画像 組合せ 問題 212225-組み合わせ 問題 解き方
1
2種類のカード A B から合わせて5枚選ぶ場合の数を求めよ.ただし,選ばれないものがあってもよいとする. この問題は普通の組み合わせとは異なり,何種類かのものから全部で何枚組み合わせの公式をつかって練習問題を解いていきます。 練習問題 1.男の子5人、女の子4人います。 この中から男の子2人、女の子2人を選ぶとき、その選び方は何通りありますか。
組み合わせ 問題 解き方
組み合わせ 問題 解き方- レンズの演習問題⑦ 組み合わせレンズの作図① PHYさん 今回は組み合わせレンズの作図の問題を扱います. 組み合わせレンズは次のステップで作図します. 手前のレンズによって 組み合わせ問題において 「少なくとも1人(1つ)〜」 を求めるときは、 組み合わせの総数 から 1人(1つ)もない場合 を引くことで求める場合が多いです。 組み合わせの総数は (1)で

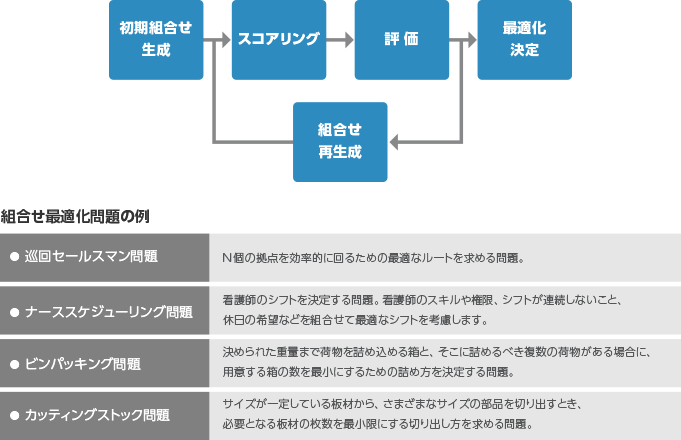
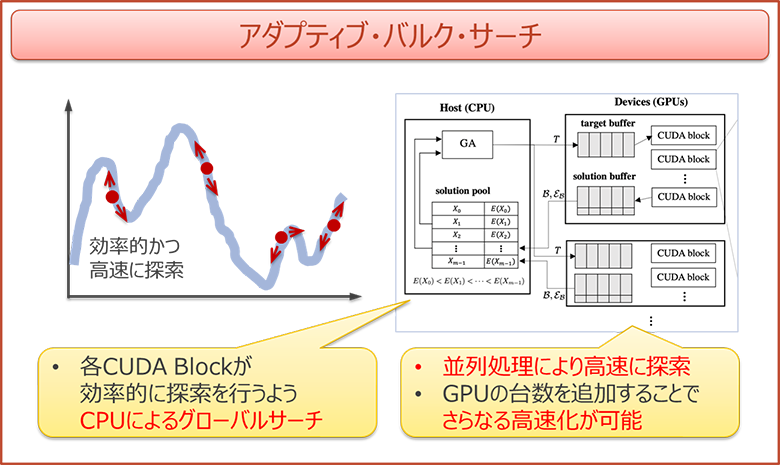
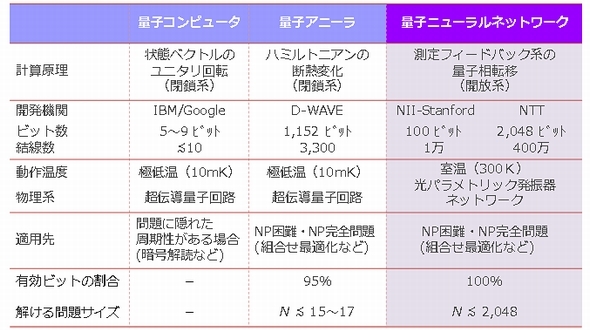
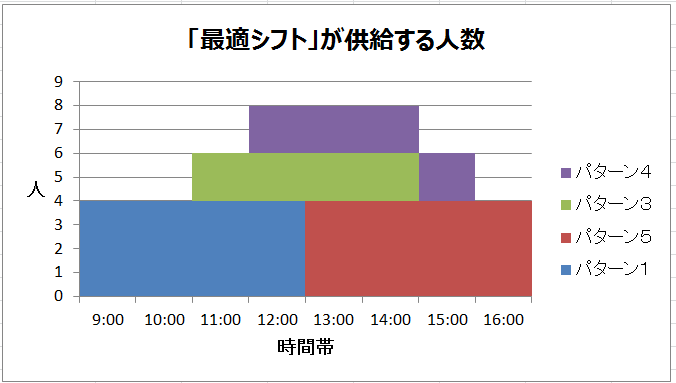
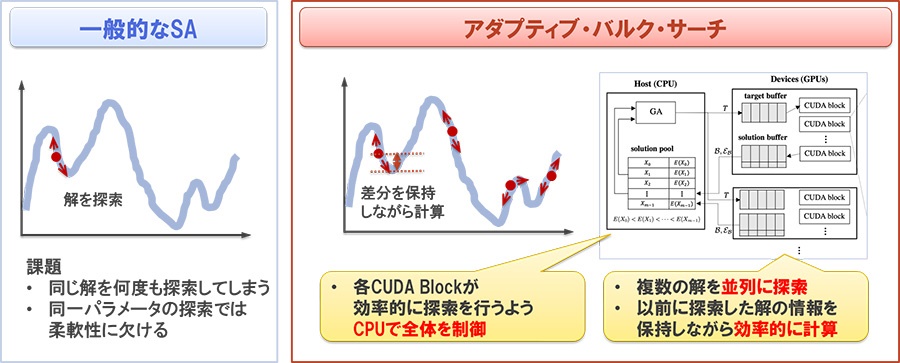
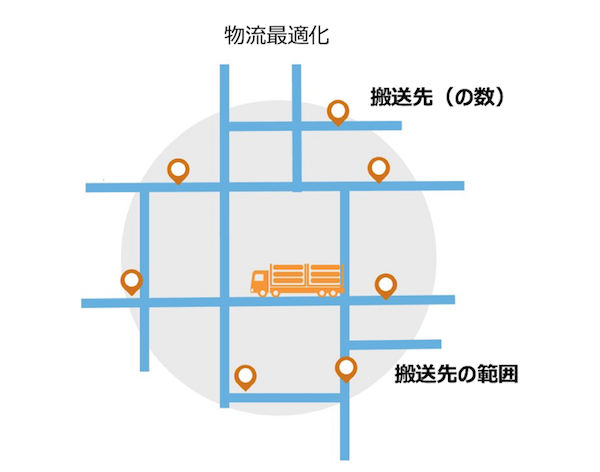
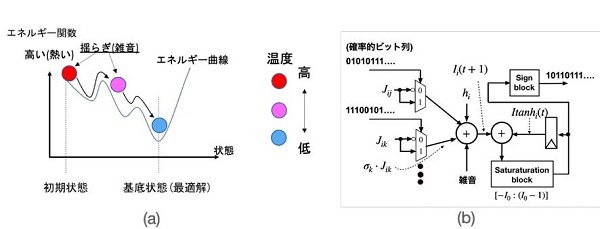
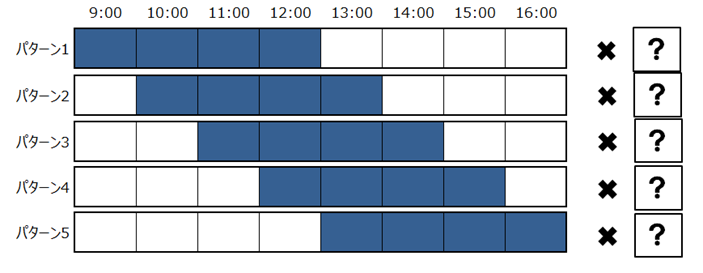
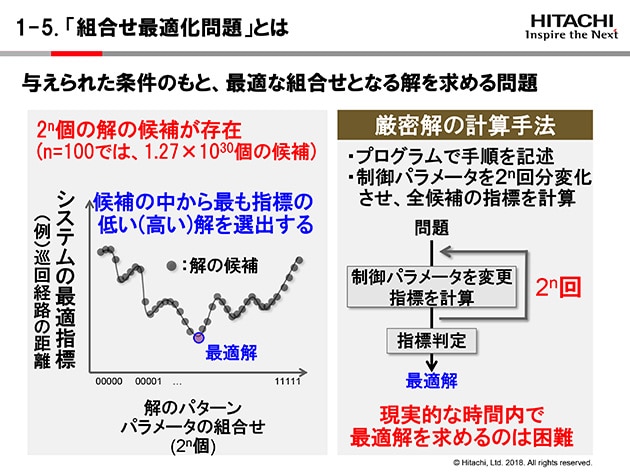
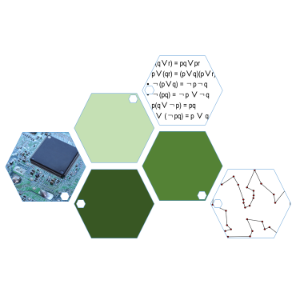
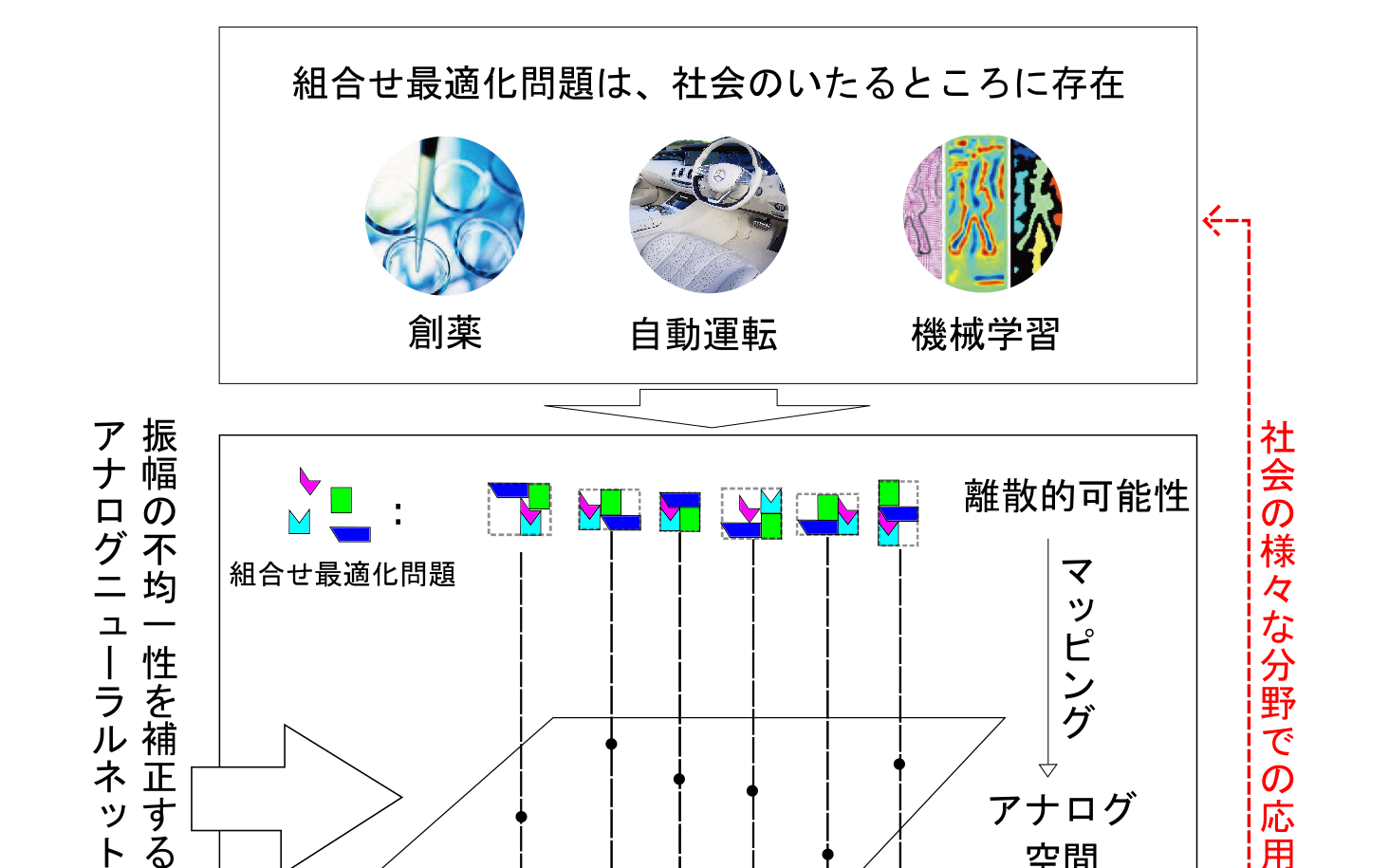
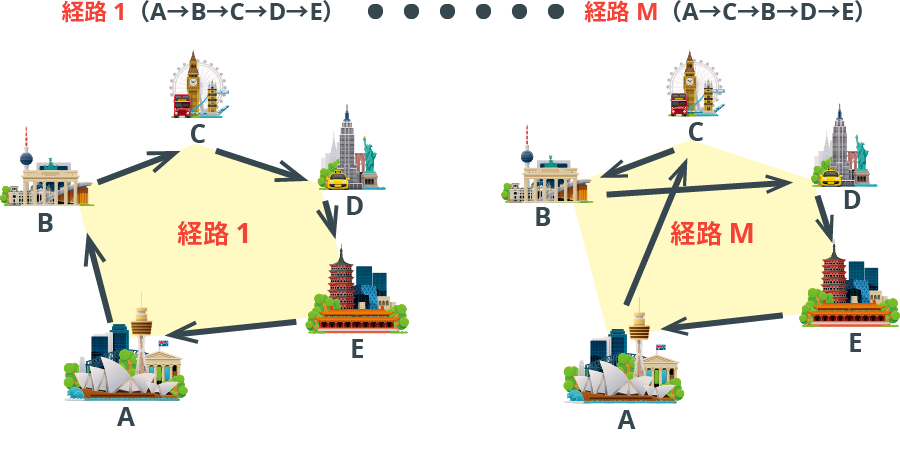
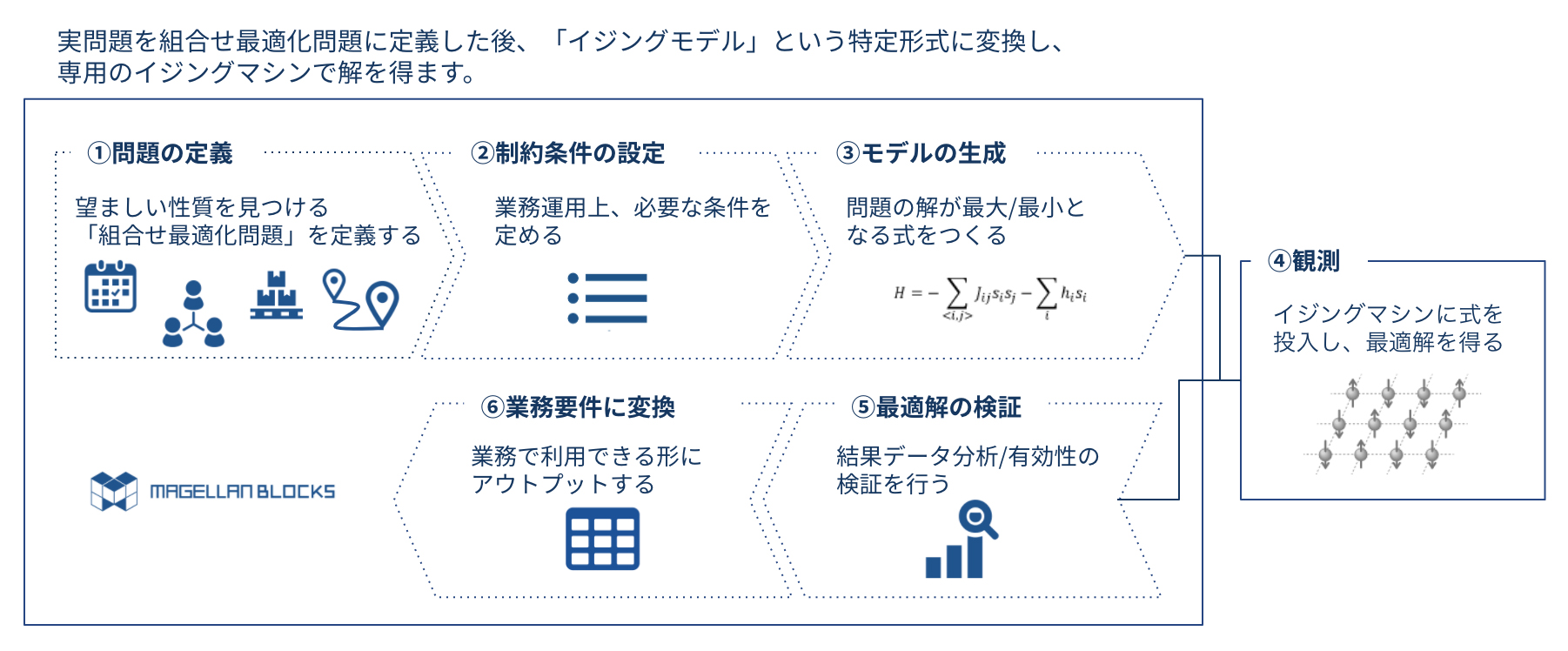
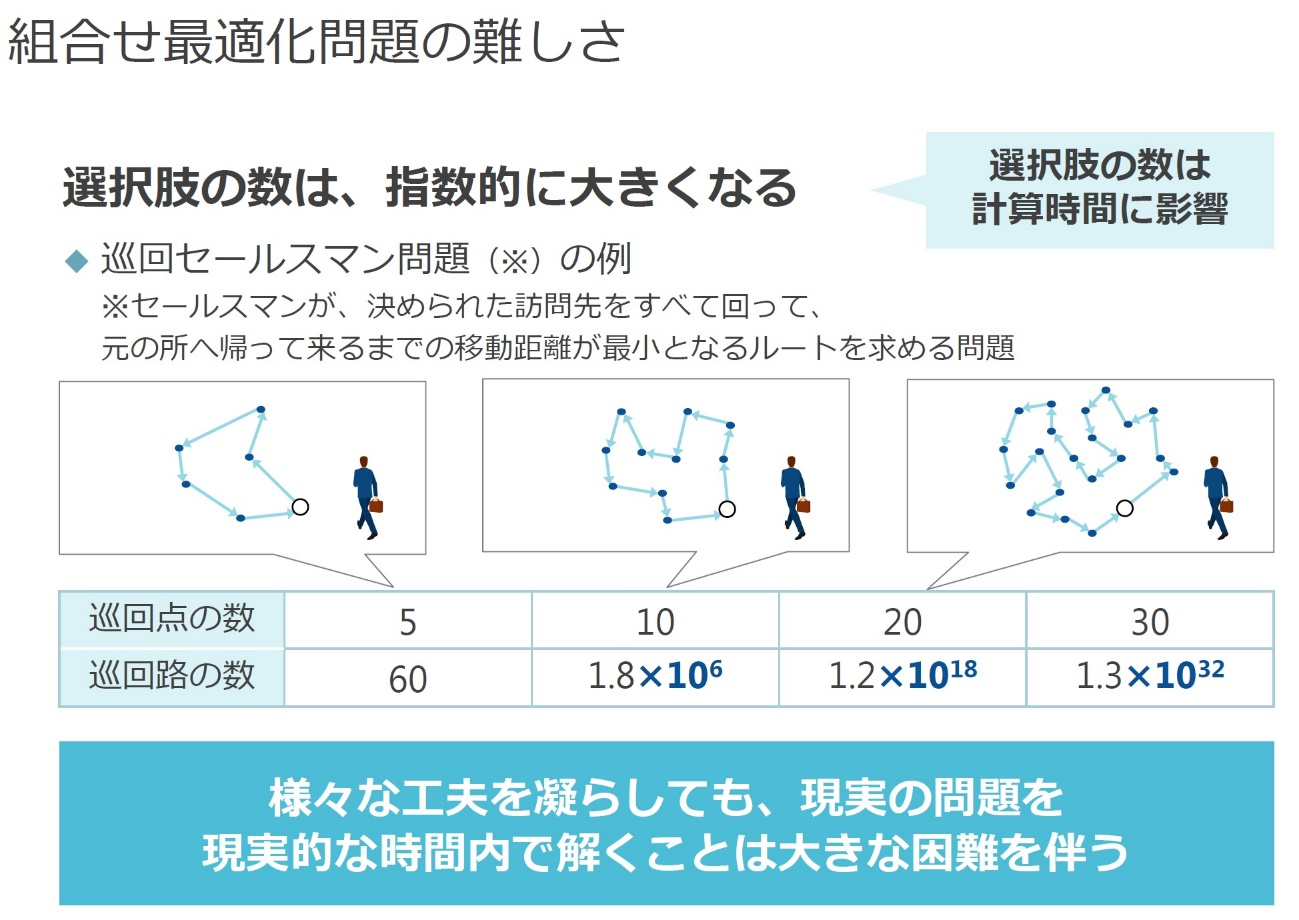
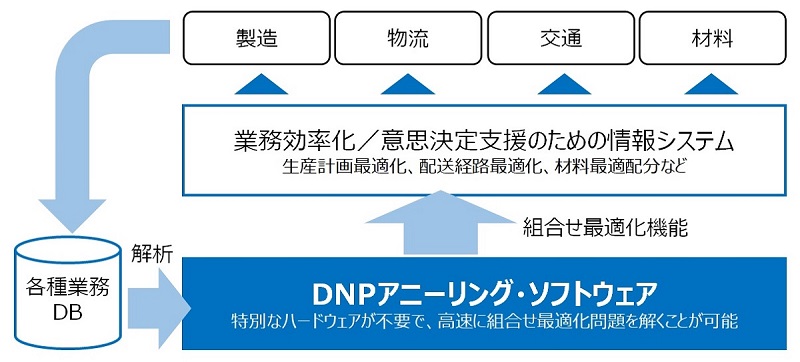
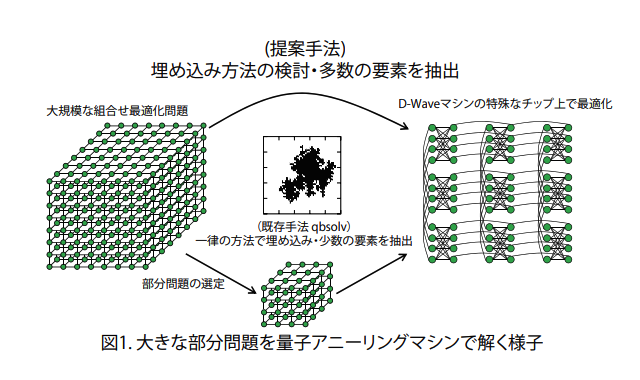
大規模な組合せ最適化問題に対する発見的解法
組み合わせ問題をJavaで Java 問題 袋に9つのボールが入っていてそのひとつひとつに1〜9の番号がついている。 ちょうどビリヤードの球が袋に9つ入っ難しくても使いこなす組合せ最適化 (2) 難しくても使いこなす組合せ最適化 (3) このコラムは「組合せ最適化問題」という難問、しかし、ビジネスの実務の世界で避けては通れない問題を紹介し、数 なのでこの問題の正しい回答は ( 5 − 1)!
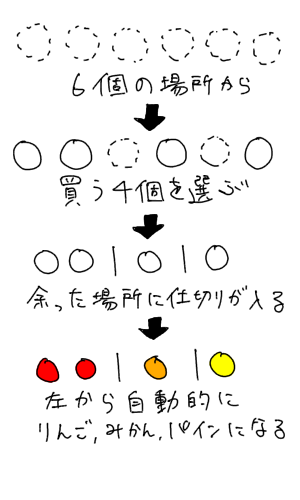
について解説していきます。 重複を許す組み合わせとは次のような問題のことですね。 問題 りんご,みかん,バナナの3種類から重複を許して,4個取り出す組み合わせは全部順列,組合せ (章末問題) ≪公式の要約≫ 順列 異なる n 個のものから,異なる r 個のものを取ってできる順列の総数( ただし, 0 ≦ r ≦ n ) n P r = n!(n−r)!nnnnnn 例 各位の数が異なる2桁の整数の組分け問題のパターン 高校数学における組分け問題は ・モノ(配られるもの)が区別できるか否か ・組(配属先)が区別できるか否か ・組(配属先)のモノの数に指定はあるか,指定がないならば,$0$ 個
組み合わせ 問題 解き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  |  |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「組み合わせ 問題 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
= 24 答えは 24 通り。 練習問題④ 上の図で各部分をそれぞれ違う色で色分けする時その場合の数を求めなさい。 解答 こういうパターンでならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるので
Incoming Term: 組み合わせ 問題, 組み合わせ 問題 高校, 組み合わせ 問題 応用, 組み合わせ 問題 解き方, 組み合わせ 問題 spi, 組み合わせ 問題 小学生, 組み合わせ 問題 中学, 組み合わせ 問題 男女, 組み合わせ 問題集, 組合せ 問題,
コメント
コメントを投稿